Dịch vụ tăng like, follow cho các MXH: FB, Instagram, Tiktok
Mục lục
Tính chất hình thoi
Hình thoi là gì
Bạn đã từng nhìn thấy một chiếc diều đang bay lượn trên bầu trời chưa? Hình dáng của chiếc diều đó rất giống với một hình học mà chúng ta sẽ cùng khám phá ngày hôm nay, đó chính là hình thoi.
Hình thoi là gì?
Hình thoi là một tứ giác mà tại đó tất cả các cạnh đều bằng nhau. Điều này có nghĩa là, nếu bạn đo độ dài của bất kỳ cạnh nào trong hình thoi, bạn sẽ thu được cùng một kết quả.
Dấu hiệu nhận biết hình thoi
Để xác định một hình tứ giác có phải là hình thoi hay không, chúng ta có thể dựa vào các dấu hiệu sau:
Tất cả các cạnh bằng nhau: Đây là dấu hiệu cơ bản và dễ nhận biết nhất.
Hai đường chéo vuông góc với nhau: Đường chéo là đoạn thẳng nối hai đỉnh đối diện của hình tứ giác. Ở hình thoi, hai đường chéo này cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.
Hai đường chéo là đường phân giác của các góc: Điều này có nghĩa là, mỗi đường chéo chia đôi góc mà nó đi qua.
Hình thoi trong cuộc sống
Hình thoi không chỉ là một khái niệm trong toán học mà còn xuất hiện trong nhiều vật dụng và công trình kiến trúc xung quanh chúng ta. Ví dụ như:
Chiếc diều: Như đã đề cập ở trên, chiếc diều có hình dạng giống hình thoi.
Mặt bàn hình thoi: Một số bàn trà, bàn ăn có mặt bàn hình thoi tạo nên sự độc đáo và hiện đại.
Gạch lát nền: Gạch lát nền hình thoi thường được sử dụng để tạo điểm nhấn cho không gian.
Các loại hạt: Một số loại hạt có hình dạng gần giống hình thoi như hạt dẻ, hạt thông.
Hình thoi là một tứ giác có tất cả các cạnh bằng nhau
Tính chất hình thoi
Hình thoi là một tứ giác đặc biệt, nơi mà mọi cạnh đều bằng nhau. Điều này tạo nên một sự cân đối hoàn hảo, khiến hình thoi trở nên nổi bật so với các hình tứ giác khác.
Định nghĩa và tính chất hình thoi cơ bản cơ bản
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
Tính chất hình thoi
Các cạnh đối song song: Giống như hình bình hành, tính chất hình thoi cơ bản là các cạnh đối diện của hình đều song song với nhau.
Các góc đối bằng nhau: Các góc đối diện của hình thoi có số đo bằng nhau.
Hai đường chéo vuông góc: Hình thoi là tứ giác có 2 đường chéo vuông góc với nhau tại trung điểm mỗi đường.
Hai đường chéo là phân giác của các góc: Mỗi đường chéo của hình thoi là phân giác của hai góc mà nó đi qua.
Hình thoi
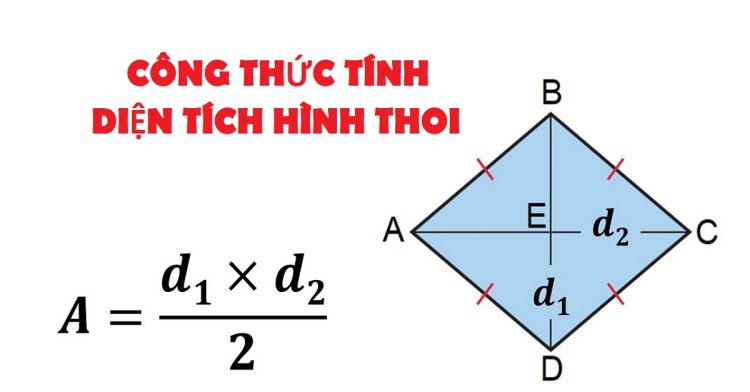
Công thức tính diện tích hình thoi
Hình thoi là một tứ giác đặc biệt có bốn cạnh bằng nhau. Các cạnh đối diện song song với nhau và hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
Công thức tính diện tích hình thoi
Có hai cách chính để tính diện tích hình thoi:
Cách 1: Dựa vào độ dài hai đường chéo
Công thức: S = (d1 × d2) / 2
Trong đó:
S: Diện tích hình thoi
d1, d2: Độ dài hai đường chéo của hình thoi
Cách 2: Dựa vào cạnh và chiều cao
Công thức: S = a × h
Trong đó:
S: Diện tích hình thoi
a: Độ dài một cạnh của hình thoi
h: Chiều cao tương ứng với cạnh a (khoảng cách từ cạnh a đến cạnh đối diện)
Ví dụ minh họa
Ví dụ 1: Một hình thoi có hai đường chéo lần lượt là 6cm và 8cm. Tính diện tích hình thoi.
Giải: S = (6 × 8) / 2 = 24 (cm²)
Ví dụ 2: Một hình thoi có cạnh dài 5cm và chiều cao tương ứng là 4cm. Tính diện tích hình thoi.
Giải: S = 5 × 4 = 20 (cm²)
Lưu ý
Đơn vị đo: Khi tính diện tích, bạn cần chú ý đến đơn vị đo của các đại lượng. Nếu các đại lượng có đơn vị đo khác nhau, cần quy đổi về cùng một đơn vị trước khi tính toán.
Hình thoi đặc biệt: Hình vuông là một trường hợp đặc biệt của hình thoi có bốn cạnh bằng nhau và bốn góc vuông. Vì vậy, công thức tính diện tích hình vuông cũng áp dụng được cho hình thoi.
Công thức hình thoi
Bài tập về hình thoi
Bài tập cơ bản
Định nghĩa:
Hình thoi là gì? Kể tên các tính chất cơ bản của hình thoi.
Vẽ một hình thoi và đánh dấu các cạnh, góc, đường chéo.
Tính toán:
Cho hình thoi ABCD có cạnh AB = 5cm, đường chéo AC = 8cm. Tính độ dài đường chéo BD và diện tích hình thoi.
Cho hình thoi MNPQ có góc M = 60 độ, đường chéo MP = 10cm. Tính độ dài cạnh MN và diện tích hình thoi.
Bài tập nâng cao
Chứng minh:
Chứng minh rằng: Trong hình thoi, hai đường chéo vuông góc với nhau và là các đường phân giác của các góc.
Chứng minh rằng: Nếu một hình bình hành có hai đường chéo vuông góc với nhau thì đó là hình thoi.
Vận dụng:
Cho hình thoi ABCD có cạnh AB = 5cm, góc A = 60 độ. Tính độ dài các đường cao của hình thoi.
Một mảnh đất hình thoi có tổng độ dài hai đường chéo là 48m. Đường chéo thứ nhất dài hơn đường chéo thứ hai 6m. Tính diện tích mảnh đất.
Bài tập mở rộng
Tìm tứ giác đặc biệt:
Cho tứ giác ABCD có AB = BC = CD = DA và góc A = 90 độ. Tứ giác ABCD là hình gì? Vì sao?
Cho tứ giác MNPQ có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường. Tứ giác MNPQ là hình gì? Vì sao?
Lưu ý
Tự mình giải các bài tập: Việc tự giải sẽ giúp bạn nắm vững kiến thức tốt hơn.
Kiểm tra lại kết quả: So sánh kết quả của mình với đáp án hoặc nhờ người khác kiểm tra giúp.
Đặt câu hỏi khi gặp khó khăn: Đừng ngần ngại hỏi thầy cô, bạn bè hoặc tìm kiếm thông tin trên mạng.
Trên đây là một số thông tin về tính chất hình thoi. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.
