Hình thoi là gì? Dấu hiệu nhận biết và tính chất hình thoi​

Tính chất hình thoi

Hình thoi là gì

Hình thoi là gì?

Hình thoi là một tứ giác mà có tất cả các cạnh bằng nhau. Điều này có nghĩa là bốn cạnh của hình thoi đều có độ dài như nhau. Ngoài ra, hình thoi còn có một số tính chất đặc biệt khác mà chúng ta sẽ tìm hiểu sau.

Hình thoi

Tính chất hình thoi

Tính chất hình thoi

Bốn cạnh bằng nhau: Đây là đặc điểm cơ bản và dễ nhận biết nhất của hình thoi.

Hai đường chéo vuông góc: Điểm đặc biệt của hình thoi là có 2 đường chéo vuông góc tại trung điểm của chúng

Các góc đối diện bằng nhau: Cặp góc đối diện trong hình thoi có số đo bằng nhau.

Hai đường chéo là đường phân giác của các góc: Mỗi đường chéo của hình thoi là đường phân giác của hai góc mà nó đi qua.

Hình thoi là một hình bình hành đặc biệt: Hình thoi có đầy đủ tính chất của hình bình hành (các cạnh đối song song và bằng nhau, các góc đối bằng nhau).

Nhận biết hình thoi

Dấu hiệu nhận biết hình thoi

Có nhiều cách để xác định một hình tứ giác có phải là hình thoi hay không. Sau đây là các dấu hiệu dễ nhận biết nhất:

Tứ giác có bốn cạnh bằng nhau:

Đây là dấu hiệu đơn giản và dễ nhận biết nhất. Nếu một tứ giác có cả bốn cạnh đều bằng nhau, chắc chắn đó là hình thoi.

Tứ giác mà có hai đường chéo vuông góc tại trung điểm của chúng:

Nếu hai đường chéo của một tứ giác cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau, thì tứ giác đó là hình thoi.

Hình bình hành có hai cạnh kề bằng nhau:

Nếu một hình bình hành có hai cạnh kề bằng nhau, tức là tất cả các cạnh của hình bình hành đều bằng nhau, thì hình đó chính là hình thoi.

Hình bình hành mà có hai đường chéo vuông góc:
Nếu một hình bình hành có hai đường chéo vuông góc với nhau, thì đó cũng là hình thoi.

Hình bình hành mà có đường chéo là đường phân giác của góc đó:

Nếu một đường chéo của hình bình hành là đường phân giác của một góc, thì hình bình hành đó là hình thoi.

Để khẳng định một tứ giác là hình thoi, bạn chỉ cần chứng minh được tứ giác đó thỏa mãn một trong các dấu hiệu trên. Việc nắm vững các dấu hiệu này sẽ giúp bạn dễ dàng nhận biết hình thoi trong các bài toán hình học.

Lưu ý: Hình thoi là một trường hợp đặc biệt của hình bình hành. Vì vậy, hình thoi cũng thừa hưởng tất cả các tính chất của hình bình hành.

Ví dụ:

Hình vuông là một trường hợp đặc biệt của hình thoi, vì hình vuông cũng có bốn cạnh bằng nhau và hai đường chéo vuông góc với nhau.

Hình thoi

Công thức tính diện tích hình thoi

Diện tích hình thoi thường có hai cách tính chính:

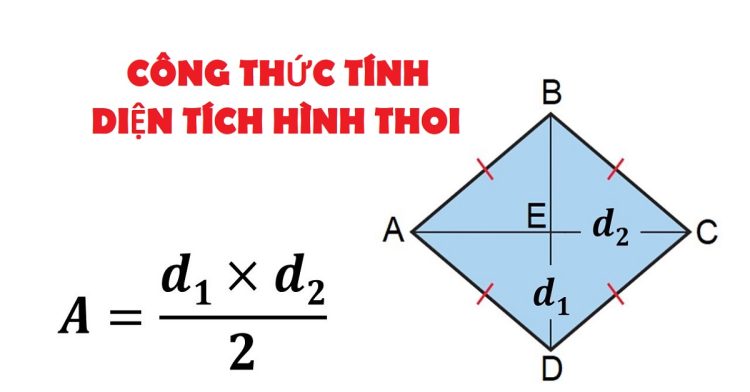
Dựa vào độ dài hai đường chéo

Công thức: S = (d1 x d2) / 2

Trong đó:

S: Diện tích hình thoi

d1, d2: Độ dài hai đường chéo của hình thoi

Vì hình thoi được chia thành 4 tam giác vuông bằng nhau, nên diện tích hình thoi bằng tổng diện tích của 4 tam giác đó. Mỗi tam giác vuông có diện tích bằng nửa tích hai cạnh góc vuông (độ dài hai đường chéo).

Dựa vào cạnh và chiều cao

Công thức: S = a x h
Trong đó:

S: Diện tích hình thoi

a: Độ dài một cạnh của hình thoi

h: Chiều cao tương ứng với cạnh a

Cũng giống như hình bình hành, diện tích hình thoi bằng tích của một cạnh với chiều cao tương ứng với cạnh đó.

Lưu ý: Chiều cao của hình thoi là đoạn thẳng vuông góc kẻ từ một đỉnh đến cạnh đối diện.

Ví dụ minh họa

Giả sử chúng ta có một hình thoi với độ dài hai đường chéo lần lượt là 6cm và 8cm. Diện tích hình thoi được tính như sau: 

S = (6cm x 8cm) / 2 = 24 cm²

Vậy diện tích hình thoi là 24 cm².

Ứng dụng của công thức tính diện tích hình thoi

Công thức tính diện tích hình thoi có nhiều ứng dụng trong thực tế, chẳng hạn như:

Tính diện tích các mảnh đất: Nhiều mảnh đất có hình dạng gần giống hình thoi.

Thiết kế các sản phẩm: Trong thiết kế đồ họa, kiến trúc, công thức này giúp tính toán diện tích các hình dạng phức tạp.

Giải các bài toán hình học: Công thức này là nền tảng để giải quyết nhiều bài toán hình học liên quan đến hình thoi.

Bài tập về tính chất hình thoi

Bài tập cơ bản về tính chất hình thoi

Cho hình thoi ABCD có AB = 5cm. Tính độ dài các cạnh còn lại.

Lời giải: Vì ABCD là hình thoi nên tất cả các cạnh đều bằng nhau. Vậy CD = DA = BC = AB = 5cm.

Cho hình thoi ABCD có góc BAC là 60 độ. Tính số đo các góc còn lại.

Lời giải: Trong hình thoi, các góc đối bằng nhau. Mà góc A = 60 độ, nên góc C = 60 độ. Tổng các góc trong một tứ giác bằng 360 độ, suy ra góc B = góc D = (360 – 60 – 60) / 2 = 120 độ.

Cho hình thoi ABCD có hai đường chéo AC = 8cm, BD = 6cm. Tính diện tích hình thoi.

Lời giải: Diện tích hình thoi bằng một nửa tích hai đường chéo. Vậy diện tích ABCD = (AC * BD) / 2 = (8 * 6) / 2 = 24 cm².

Bài tập nâng cao về tính chất hình thoi

Cho hình thoi ABCD có cạnh AB = 5cm, đường cao AH = 4cm (H thuộc CD). Tính độ dài đường chéo AC.

Gợi ý: Sử dụng định lý Pytago trong tam giác vuông AHC để tính AC.

Cho hình thoi ABCD có góc A = 60 độ, cạnh AB = a. Tính độ dài các đường chéo AC và BD.

Gợi ý: Chia hình thoi thành 4 tam giác đều.

Cho hình thoi ABCD có diện tích bằng 24cm², đường chéo AC = 6cm. Tính độ dài đường chéo BD và chu vi hình thoi.

Bài tập vận dụng về diện tích hình thoi

Một mảnh đất hình thoi có chu vi là 100m. Biết một đường chéo của hình thoi dài 30m. Tính độ dài đường chéo còn lại và diện tích mảnh đất.

Một chiếc diều hình thoi có hai đường chéo lần lượt là 80cm và 60cm. Tính diện tích chiếc diều đó.

Trên đây là một số thông tin về hình thoi và các tính chất của hình thoi. Hi vọng chỉ cần các bạn sẽ có cho mình thông tin hữu ích.