Dịch vụ tăng like, follow cho các MXH: FB, Instagram, Tiktok
Mục lục
Tính chất hình thoi
Dấu hiệu nhận biết hình thoi
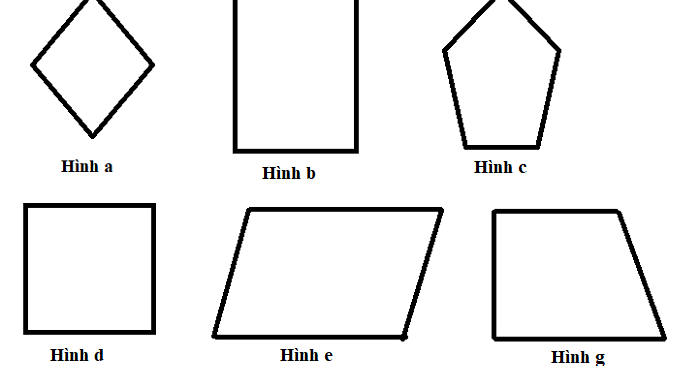
Hình thoi là một hình tứ giác đặc biệt, có nhiều tính chất thú vị. Để nhận biết một hình tứ giác có phải là hình thoi hay không, bạn có thể dựa vào các dấu hiệu sau:
Các dấu hiệu chính
Bốn cạnh bằng nhau: Đây là dấu hiệu đơn giản và dễ nhận biết nhất. Nếu một tứ giác có cả bốn cạnh đều bằng nhau thì chắc chắn đó là hình thoi.
Hai đường chéo vuông góc với nhau: Đường chéo của hình thoi luôn cắt nhau tại trung điểm và vuông góc với nhau.
Hai đường chéo là đường phân giác của các góc: Mỗi đường chéo của hình thoi đều là đường phân giác của hai góc mà nó đi qua.
Hình bình hành có hai cạnh kề bằng nhau: Nếu một hình bình hành có hai cạnh kề bằng nhau thì nó cũng là hình thoi.
Hình bình hành có hai đường chéo vuông góc: Hình thoi cũng có thể là hình bình hành có 2 đường chéo vuông góc với nhau
Tổng kết các dấu hiệu nhận biết hình thoi
Tứ giác có 4 cạnh bằng nhau.
Tứ giác có hai đường chéo vuông góc với nhau.
Tứ giác có hai đường chéo là đường phân giác của các góc.
Hình bình hành có hai cạnh kề bằng nhau.
Hình bình hành có hai đường chéo vuông góc.
Ví dụ
Nếu bạn có một tứ giác và bạn đo được bốn cạnh của nó đều bằng nhau, hoặc bạn thấy hai đường chéo của nó vuông góc với nhau, thì bạn có thể kết luận rằng đó là một hình thoi.
Hình thoi
Tính chất hình thoi
Hình thoi là một tứ giác đặc biệt với nhiều tính chất thú vị. Dưới đây là những tính chất hình thoi:
Các cạnh và góc
Bốn cạnh bằng nhau: Đây là đặc điểm cơ bản nhất của hình thoi.
Các góc đối nhau bằng nhau: Tương tự như hình bình hành.
Hai đường chéo vuông góc với nhau: Đường chéo thứ nhất vuông góc với đường chéo thứ hai và cắt nhau tại trung điểm của mỗi đường.
Các đường đặc biệt
Hai đường chéo là các đường phân giác của các góc: Mỗi đường chéo chia đôi góc mà nó đi qua.
Các cạnh của hình thoi là các đường phân giác của các góc ngoài: Mỗi cạnh chia đôi góc ngoài tại đỉnh đối diện.
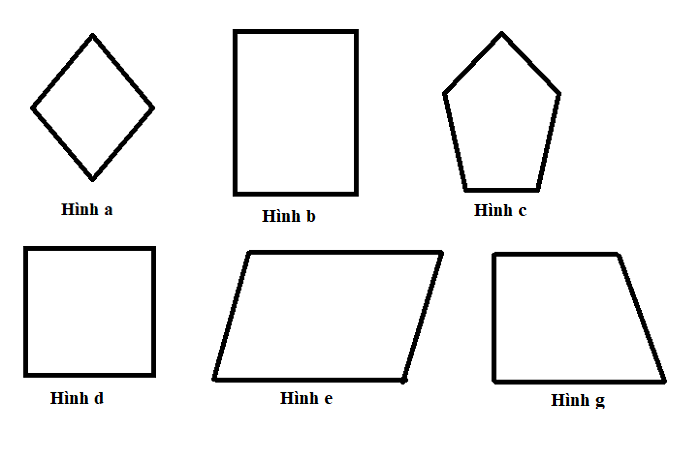
Dấu hiệu nhận biết hình thoi
Công thức tính diện tích hình thoi
Diện tích hình thoi được tính bằng một nửa tích của hai đường chéo.
Công thức
S = (d1 x d2) / 2
Trong đó:
S: Diện tích hình thoi
d1, d2: Độ dài hai đường chéo của hình thoi
Ví dụ:
Nếu một hình thoi có hai đường chéo lần lượt là 6cm và 8cm, thì diện tích của hình thoi đó là:
S = (6cm x 8cm) / 2 = 24 cm²
Tại sao lại có công thức này?
Để hiểu rõ hơn về công thức này, bạn có thể chia hình thoi thành 4 tam giác vuông bằng nhau. Diện tích của mỗi tam giác vuông bằng một nửa tích của hai cạnh góc vuông (đây chính là hai nửa đường chéo của hình thoi). Khi cộng diện tích 4 tam giác vuông lại, ta sẽ được công thức tính diện tích hình thoi như trên.
Ngoài ra, bạn có thể tính diện tích hình thoi bằng công thức:
S = a x h
Trong đó:
a: Độ dài một cạnh của hình thoi
h: Chiều cao tương ứng với cạnh a
Lưu ý: Chiều cao của hình thoi là đoạn thẳng vuông góc kẻ từ một đỉnh đến cạnh đối diện.
Ứng dụng:
Công thức tính diện tích hình thoi được sử dụng rộng rãi trong các bài toán hình học, đặc biệt là khi tính diện tích các hình phẳng phức tạp được ghép từ nhiều hình thoi.
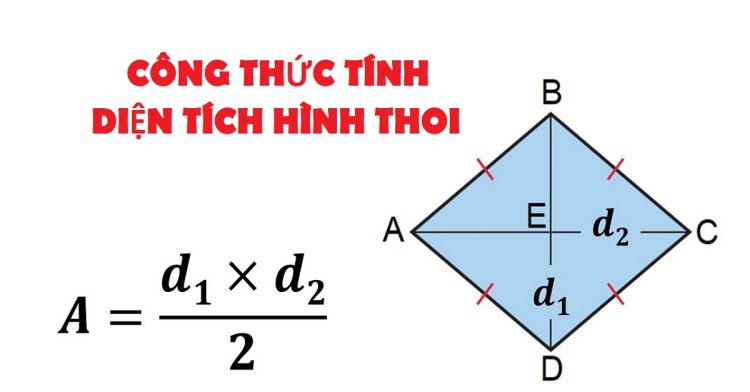
Công thức diện tích hình thoi
Bài tập về tính chất hình thoi
Dưới đây là một số bài tập về tính chất hình thoi, từ cơ bản đến nâng cao, kèm theo lời giải chi tiết:
Bài tập cơ bản
Bài 1: Cho hình thoi ABCD có cạnh AB = 5cm. Tính chu vi hình thoi ABCD.
Lời giải:
Vì hình thoi có 4 cạnh bằng nhau nên chu vi hình thoi ABCD = 4 x AB = 4 x 5 = 20 (cm).
Bài 2: Cho hình thoi ABCD có hai đường chéo AC = 6cm, BD = 8cm. Tính diện tích hình thoi ABCD.
Lời giải:
Diện tích hình thoi ABCD = (AC x BD) / 2 = (6 x 8) / 2 = 24 (cm²).
Bài 3: Cho hình thoi ABCD có góc A = 60°. Tính số đo các góc còn lại của hình thoi.
Lời giải:
Vì ABCD là hình thoi nên các góc đối nhau bằng nhau. Mà góc A = 60° nên góc C = 60°.
Tổng các góc trong một tứ giác bằng 360°, suy ra góc B = góc D = (360° – 60° – 60°) / 2 = 120°.
Bài tập nâng cao
Bài 4: Cho hình thoi ABCD có cạnh AB = 5cm, đường cao AH = 4cm. Tính độ dài đường chéo AC.
Lời giải:
(Bài toán này cần sử dụng định lý Pytago và tính chất của hình thoi)
… (Bạn thử giải bài toán này nhé, nếu gặp khó khăn hãy hỏi mình)
Bài 5: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AC = 10cm, BD = 12cm. Tính độ dài cạnh AB và diện tích tam giác AOB.
Lời giải:
(Bài toán này kết hợp tính chất hình thoi và định lý Pytago)
… (Bạn thử giải bài toán này nhé, nếu gặp khó khăn hãy hỏi mình)
Một số bài tập tự luyện
Cho hình thoi ABCD có góc A = 60°. Kẻ BH vuông góc với AD (H thuộc AD). Chứng minh tam giác AHB đều.
Cho hình thoi ABCD có cạnh AB = a. Tính độ dài các đường chéo AC và BD theo a, biết góc A = 60°.
Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo. Kẻ OM vuông góc với AB tại M, ON vuông góc với BC tại N. Chứng minh: MN // AC.
Lưu ý:
Để giải các bài toán về hình thoi, bạn cần nắm vững các tính chất cơ bản của hình thoi, định lý Pytago và các kiến thức về tam giác.
Vẽ hình sẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra lời giải.
Kiểm tra lại kết quả sau khi làm bài.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu, video hướng dẫn trên mạng để hiểu sâu hơn về hình thoi nhé!
Trên đây là một số thông tin về hình thoi, tính chất và công thức của hình thoi. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.
